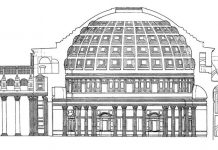
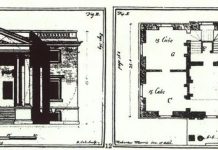
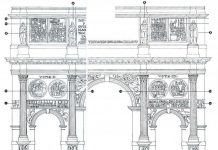
Сначала там, где я должен сделать рйсунок, я черчу четырехугольник с прямыми углами такого размера, какого я хочу [ABD4], и принимаю его за открытое окно, откуда я разглядываю то, что на нем будет написано, и здесь же я определяю рост человека, нужный мне для моей картины, и делю рост этого человека на три части, каждую из которой я для себя принимаю пропорциональной той мере, которая называется локтем. Этими локтями я делю нижнюю лежащую линию [А4] четырехугольника на столько частей, сколько она их вмещает, и эта же линия будет для меня пропорциональной ближайшему и всякому другому равностоящему поперечному протяжению, видимому на полу [в итал. ред. ed emmi questa linea medesima proportionale a quella ultima quantita quale prima mi si tra- verio innanzi; лат. ред: a mihi quidem haec ipsa jacens quadranguli linea est proximiori et nequidistanti in pavimento visae quantitati propor- tionalis]. Затем внутри этого четырехугольника \ABD4], там, где мне вздумается, я устанавливаю точку, которая занимала то место, куда ударяет центральный луч, и поэтому я называю эту точку центральной [С]. Хорошо будет поместить эту точку над нижней лежащей линией четырехугольника [А4] не выше роста того человека, которого мне предстоит написать [то есть АЕ = 3, т. к. А1 = Уз роста человека], ибо таким образом как зритель, так и видимые написанные вещи кажутся находящимися на одном уровне. Итак, поместив центральную точку [С], как я сказал, я провожу из нее прямые линии к каждому делению на лежащей внизу линии четырехугольника [то есть линии СА, Cl, С2, СЗ, С4]. Эти проведенные линии показывают мне, каким образом изменяется каждое поперечное протяжение, как бы уходя в бесконечность. А для того чтобы установить последовательность поперечных протяжений, я держусь такого порядка. Я беру маленькую площадь, провожу на ней прямую линию [PTJ] и делю ее на части, подобные тем, на которые делил лежащую нижнюю линию четырехугольника [ABD4\. Затем наверху я ставлю точку [О], на той же высоте от этой линии [PTJ], на которой я помещал в четырехугольнике центральную точку [С] над его нижней линией \А4], и из этой точки я провожу к линии к каждому делению, обозначенному на первой линии [PTJ], Затем я произвольно устанавливаю расстояние глаза от картины [ОС] и провожу, как говорят математики, перпендикулярную линию [LCT], пересекающую любую встречную линию [01,02, 03, 04]… Эта перпендикулярная линия при пересечении с другими линиями дает мне, таким образом, последовательность всех поперечных протяжений [1, 2, 3, 4]. И, таким образом, у меня в картине оказываются обозначенными все параллели, то есть квадратные локти пола. Признаком же того, что они правильно начерчены, будет, если одна и та же прямая линия окажется продолжением диаметров всех квадратов, начерченных на картине».
Помещенные выше чертежи заимствованы из комментария Людвига к «Книге о живописи» Леонардо да Винчи.68 В старых изданиях сочинения Альберти дан чертеж, не соответствующий тексту. Такой же неправильный чертеж — в издании Бонуччи. Ошибочен и чертеж в издании Яничека. Поэтому для Яниче- ка остается непонятным, о какой перпендикулярной линии говорит Альберти69 и каким образом проведение диагоналей служит проверкой правильности построения.70
Имеются у него и неточности в переводе.71 Естественно, что Яничек вынужден был предположить искажения в тексте.72
Между тем, как нетрудно видеть, текст Альберти ясен. Следует лишь отрешиться от взгляда, будто Альберти было известно то построение, которое у немецких исследователей носит название Dis- tanzpunktverfahren, то есть построение при помощи так называемой точки расстояния.
Справедливо указывалось,74 что условием альбертиевского построения является разглядывание и измерение тел со всех сторон,75 в то время как позднейший способ менее нагляден.76
Словом, при «пластическом восприятия» Альберти для него не существовало разрыва между математической теорией перспективы и видимой реальной действительностью. Теория перспективы имела для него в первую очередь объективно-познавательное значение.
Между тем Л. Олынки в своей статье «О геометрическом духе в литературе и искусстве» утверждает диаметрально противоположное.77 Анализируя художественные явления Ренессанса, Олынки замечает: «Если этот стиль пространственности, как часто случается, называют реалистическим, то таким названием определяется не его существо, а его действие на наблюдателей, притом определяется посредством слишком расплывчатого понятия и в его воздействии только на таких наблюдателей, которые подходят к нему именно с этой, заранее предвзятой установкой »,78 На деле же, по Ольш- ки, в эпоху Ренессанса «действительный, эмпирический мир приспособляясь к идеальной, хотя и не вымышленной действительности, наглядной и тем не менее абстрактной».79 «Живописное распределение фигур и пространства включается в мир строжайших закономерностей, который в себе самом содержит мерило своего Gehalt’a и своей красоты. В основе этого евклидовского воззрения на пространство лежит сознание всеобщей, первичной и объективной значимости такого пространственного воззрения».80 Дальше Олыпки определяет это воззрение как «платоническое»: геометрические фигуры суть «символические формы мирового разума, и их приноровление к формам искусства сообщает искусству красоту и благородство божественной законченности и порядка». Поэтому общеизвестное «негалантное» восклицание Паоло Уччелло поздней ночью в ответ на приглашение жены идти спать — «Какая чудная вещь перспектива!» — Олынки истолковывает в том же смысле: «Denn sie [die Perspektive] erhob den Geist zur ewigen Schonheit, die der Kiinstler im Antlitz seiner braven Frau wahrscheinlich nicht mehr zu entdecken vermochte».