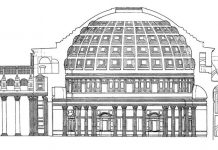
В атмосфере флорентийского платонизма, теологизируя теоремы Евклида и восхваляя чудесные свойства дивного отношения, монах Лука Пачоли заговорил о «божественной пропорции». Введение термина «золотое сечение» иногда приписывали Кеплеру, однако по недоразумению. Кеплер говорит: «Существует два сокровища в геометрии: одно есть отношение диагонали прямоугольника к сторонам, другое — деление линии в крайнем и среднем отношении. Из первого вытекает построение куба, пирамиды и октаэдра, а из второго — построение додекаэдра и икосаэдра». И далее: «Обе теоремы — бесконечной полезности и потому в высшей степени драгоценны, и тем не менее между обоими существует большая разница. Ибо первую, гласящую, что стороны прямоугольника, будучи возведены в степень, равны квадрату линии, противолежащей прямому углу, — эту теорему, говорю я, ты справедливо уподобишь куску золота, вторую, о пропорциональном сечении, назовешь драгоценным камнем. Ведь она, хотя и прекрасна сама по себе, однако без первой ничего не стоит; но зато она движет наше знание дальше тогда, когда первая покидает нас, уже продвинувшихся до некоторой степени по нашему пути, а именно движет к обнаружению и определению стороны десятиугольника и родственных качеств».37 38
Этот малоизвестный и, насколько я знаю, не переводившийся на русский язык текст весьма важен во многих отношениях. Он не только с очевидностью показывает, что термин «золотое сечение» не принадлежит Кеплеру и что, по Кеплеру, «золотое сечение» следовало бы, скорее, назвать «алмазным». Он свидетельствует, что во времена Кеплера, как и раньше, главное свое приложение «золотое сечение» находило в теории многогранников и прославлялось не как самодовлеющее эстетически совершенное отношение, а как техническое средство к достижению определенных целей — установлению связи между правильными многогранниками.
Показательно, что термин «золотое деление», aurea divisio, встречается уже гораздо раньше, хотя, правда, и в другом значении, но в этом случае эпитет «аигеа» указывает на техническую легкость и практическое удобство. Анонимное сочинение об абаке, дошедшее до нас в рукописи середины XII в., различает «золотые» и «железные» приемы деления чисел, называемые так потому, что первые легки для понимания и «приятнее золота», а вторые, напротив, трудны и тяжелы: «Dicuntur aureae divisiones eo quod ad intelligenium faciles et super auri gratiam sint delectabiles, sicut econtra ferreae quae sunt nimis graves quasi ferri duriciam preponderantes».38,6)
Таким образом, и здесь «золотому сечению» не отводится первого места. Лишь в эпоху Возрождения на почве платоновской натурфилософии и, в частности, «Тимея» создалось новое, чисто умозрительное отношение к «золоту», которое, разумеется, в известной мере могло повлиять и на архитектурную практику.
В мои задачи не входит детальный анализ вопроса о роли «золотого сечения» в трактатах других теоретиков Ренессанса, кроме Альберти. Не могу не отметить, однако, что попытки обнаружить знакомство с системой «золотых» закономерностей и пользование ею в трактате Виньолы не представляются убедительными. В комментарии к русскому изданию40 Г. Н. Емельянов основывает подобное утверждение на построении тосканского интерколумния и утонения тосканской колонны у Виньолы. Аргументация в первом случае ведется так. По Витрувию, интерколумний евстиля равен 4 Уг модулям, по Виньоле, интерколумний тосканского ордера составляет 42/з модуля, дорического — 5 Уг модулей. Отношение высоты колонны к ин- терколумнию равно во всех трех случаях 14:4 Уг, 14 : 4 2/з и 16 : 5Уг или 4,110, 3,004 и 2,909. Разность между 3,110 и 2,909, равная 0,201, будучи разделена в отношении первой «функции» «золотого сечения» 0,528 и 0,472, дает 0,106 и 0,095. Эти две последние величины равны разностям между первой и второй величиной и между второй и третьей. Отсюда делается вывод, что Виньола пришел к своей величине тосканского интерко- лумния, взяв некое среднее между евстилем Витрувия и дорическим интерколумнием своего же собственного канона: между евстилем и тосканским интерколумнием разность равна большой «функции», а между тем же тосканским интерколумнием и дорическим — малой «функции».41
Аналогично рассуждение ведется во втором случае, по поводу утонения тосканской колонны. По Витрувию, утонение тосканской колонны равно 3 : 4 или 0,750, утонение дорической 5:6 = 0,833. По Виньоле, утонение дорической колонны равно также 5:6, а утонение тосканской равно отношению 1 модуля 7 парт к двум модулям, то есть 0,792. Комментатор полагает, что эта величина 0,792 получается как средний результат между 0,750 и 0,833, при делении разности 0,083 в отношении «второй производной функции золотого сечения» 0,507 и 0,493, что дает 0,042 и 0,041, разность между первой величиной и средней и разность между средней и последней.42
Однако оба результата, на первый взгляд поразительные, получаются только как следствие оперирования десятичными дробями, которыми Виньола не оперировал. Попробуем обойтись без них, и результат будет другой. Прежде всего отношение высоты колонны к интерколумнию в случае тосканского ордера будет равно в точности трем, а не 3,004. В самом деле, 14 : 4 2/з = 3. Поэтому нет необходимости искать для него каких-либо других объяснений: это отношение вполне в духе Виньолы, «любителя целых чисел». Но если даже продолжить рассуждение так, как это было сделано выше, мы
Разность между обоими составляет 2%э, а отношение между слагающими ее разностями равно 11:9. При переводе на десятичные дроби это дает 0,550 и 0,450, а не 0,528 и 0,472. Еще проще обстоит дело во втором случае. Утонение тосканской колонны, по Витрувию — 3/4, дорической колонны, по Виньоле — 5/в. Отношение 1 модуля 7 парт к двум модулям в тосканском ордере Виньолы равно : 24 = 19: 24. Но 19/24 есть точное среднее арифметическое 3/4 и %; иными словами, разности между 5/е и 19/24, с одной стороны, и 19/24 и % — с другой, равны друг другу в точности, то есть относятся друг к другу как 0,5 к 0,5, а не как 0,507 к 0,493. Виньола и здесь не изменил своему «пафосу простых чисел».
За промежуток времени свыше трех с половиной столетий, с момента выхода в свет трактата Пачоли в 1509 г. до трудов Адольфа Цейзинга в 50-х гг. XIX в., не было, насколько мне известно, опубликовано ни одного сочинения, специально посвященного «золотой», или «божественной», пропорции. В области теории — несомненный разрыв традиции, и потому исследователи — как современники Цейзинга, так и последующие — имели право называть его создателем новой математической эстетики.43
Дело не только в степени знакомства Цейзинга со своими предшественниками, дело в принципиально новом подходе к проблеме. Искания Цейзинга относятся к началу того периода в истории эстетики, который характеризуется стремлением построить эстетику в качестве «строгой науки» по образцу математического естествознания, иными словами, отыскать законы красоты, основанные на числах, подобно математическим законам природы. В отличие от старой «метафизической» теории прекрасного эта эстетика должна была, по мысли своих создателей, быть эмпирической и экспериментальной и начинать свои исследования с простейших случаев и простейших элементов. Логически неизбежным шагом отсюда был переход к подмене конкретного анализа абстрактным рассмотрением вырванных из художественного контекста элементов и далее — применение ложно понятого статистического метода к явлениям искусства. Математические формулы и статистические подсчеты, придавая изложению характер научной аподиктичности, убеждали, казалось, что теперь-то, наконец, эстетика из «метафизического тумана» выходит на верную дорогу математического естествознания и экспериментального наблюдения.44 Создатели экспериментальной психологической эстетики превосходно знали, что простейшая форма в сочетании с новыми элементами воспринимается иначе, чем сама по себе: именно они, например, пустили в широкое обращение общеизвестный пример параллельных линий, пересеченных косыми линиями и перестающих восприниматься как параллельные, или дуг, не встречающихся своими концами. И тем не менее именно в экспериментально-психологической эстетике Фехнера и его школы, продолжившей исследования Цейзинга, внимание к простейшим формам как таковым приобрело исключительное значение. От статистического изучения форматов книг, визитных карточек, плиток шоколада, пряников, кирпичей и т. д. было еще очень далеко до сложного художественного целого.45 А что именно абстрактное изучение простейших форм — с тем, чтобы лишь впоследствии перейти к изучению более сложных, — было ведущим и руководящим, видно из собственных невольных признаний Фехнера, который рассказывает о том, какое насилие над психикой испытуемых приходилось ему производить, исследуя вопрос о сравнительной красоте различных видов прямоугольников. «Большинство заявляло с самого начала, что в зависимости от своего применения тот или иной прямоугольник может оказаться самым приятным. Я с этим соглашался, но спрашивал все-таки, не могут ли они признать один из этих прямоугольников более приятным, более удовлетворительным, гармоничным, изящным, считаясь с присущим ему отношением сторон, и какой из них они предпочли бы в качестве средней наиболее приятной формы ». «Несмотря на это предписание, — оговаривает Фехнер, — а именно не думать об определенном применении, все-таки, по всей вероятности, мысли об этом частью невольно продолжали играть свою роль при оценке».* 46 После таких психических репрессий, признает Фехнер, «начиналось довольно продолжительное колебание. И если ранее даже высказывались в пользу определенного прямоугольника, иногда позднее при том же эксперименте, поправляясь, отдавали предпочтение другому или оставались в нерешительности перед двумя, тремя и даже четырьмя прямоугольниками»,47 Результат всего этого тот, что такие эксперименты и могут иметь силу лишь в отношении к абстрактным прямоугольникам, отделенным пропастью от конкретного мира. Если теоретикам вплоть до XVI в. «золотое сечение» служило прежде всего техническим приемом, чтобы достигнуть определенных соотношений между элементами, и не рассматривалось как нечто ценное само по себе9 то в середине XIX в. оно все более и более становилось той целью, тем гчгка той, к которому устремляется деятельность художника. Пропорции из средства выразительности превращались в фетишизированные «объективные данности», которые не только не изучались в связи с выразительными моментами, но, наоборот, всячески изолировались от них при экспериментировании.
Я не буду останавливаться на той второй волке интереса к «золотому сечению», которая отразилась в книгах Хэмбиджа, Гика и др. Авторы этого направления, продолжая фетишизацию числа, геометрии и пропорций, привнесли ко всему прочему «корыстные» практические интересы, стремясь механически решить сложнейшие вопросы художественного творчества путем отыскания «забытых рецептов и формул».
Совершенно очевидно отличие этой «науки» о пропорциях от той концепции пропорций, которая отличала теоретиков Возрождения и, в частности, Альберти. Как прав был Буркгардт, когда писал: «Auf rein mathematischem Wege kann man nie zu durchgreifenden Regeln gelangen, weil ausser den Proportionen auch die starkere oder schwache- re Plastik der For men die Wirkung entscheiden hilft, sodass bei densel- ben Verhaltnissen ein Bau schlanker oder schwerer erscheinen kann. Es ware zu wunschen, dass ein Wort existierte, welches ausdriicklich die Verhaltnisse und die Plastik zugeich umfasste… Die Verhaltnisse in ihrer Beziehung zu den Formen und diese zu jenen bleiben… Sache der hochsten und feinsten kiinstlerischen Vermogen»,48