Заметим, что квадратура круга была лишь частным видом общего понятия «квадратуры», приведения к квадрату. В случае квадратуры прямоугольников задача заключалась в нахождении средней пропорциональной, иначе говоря в нахождении того связующего «среднего», которое легло в основу всей философии архитектурных пропорций у Альберти., что это — нахождение среднего ».9)) У него же: «Что такое квадратура ? Построение равносторонней прямоугольной фигуры, равной неравносторонней. Такое определение указывает лишь следствие. Утверждающий же, что квадратура есть нахождение среднего, обозначает причину действия».37
Итак, интерес Альберти к вопросам квадратуры круга был логически последовательным этапом в развитии всей его философии архитектурных пропорций.38
Альберти чаще всего пользовался не формально-логическими дефинициями, а определениями по аналогии. Подобные определения устанавливали связь и переходы между понятиями и явлениями и служили средством открытия новых истин, то есть имели для него значение эвристическое. Такое широкое пользование аналогиями, как я уже сказал, роднит Альберти с ведущими направлениями научной и философской мысли Возрождения.39
Наоборот, оно противопоставляет Альберти основным традициям школьной логики и схоластического мышления. Мишель справедливо отмечает у Альберти «почти полное забвение старой силлогистики, в которую однако он должен был быть посвящен своими падунскими и болонскими наставниками неправильно указано, что имеется в виду арифметическое среднее, хотя формула и дана им правильная X = Уа5. syllogistique, a laquelle il dut pourtant etre initie par ses maitres de Padoue et de Bologne)».40 Один пример даже не силлогизма, а цепи силлогизмов в форме сорита, Мишель указывает в сочинении «О семье»: «Но самое существо такого рассуждения внушает недоверие, которое усиливается архаическим характером Джаноццо [в уста которого это рассуждение вложено. — В. 3.]: вероятно, автор забавляется, и его сорит стоит в известном родственном отношении к сориту лисы у Монтеня »,41
Не могу в заключение не привести блестящий отрывок из сочинений Кеплера, прекрасно иллюстрирующий, какое огромное значение люди Ренессанса придавали методу аналогий. Кеплер говорит о переходе от прямой через бесконечное число гипербол к параболе, далее — через бесконечное число эллипсов — к кругу, ибо «из всех эллипсов самый острый — парабола, самый тупой — круг». «Итак, — продолжает Кеплер, — противоположные термины — круг и прямая, там — чистая кривизна, здесь — чистая прямизна. Находящиеся в промежутке гипербола, парабола, эллипс причастны и прямому и кривому: парабола — в одинаковой мере, гипербола — более прямизне, эллипс — более кривизне». И за этими рассуждениями, поясняемыми при помощи чертежа,следует восторженное восклицание: «Да, я люблю, очень люблю аналогии, самых преданных моих наставниц, сопричастниц всех тайн природы; и в геометрии должно следовать им особенно, ибо хотя они путем странных словесных оборотов объемлют бесконечное число случаев, заключающихся между крайними их пределами и серединой, но зато воочию являют всю сущность какого-либо предмета».42
Касательная к кругу есть секущая, точки пересечения которой совпадают, асимптота есть касательная к бесконечно далекой точке — можно было бы привести множество других математических параллелей к аналогичным определениям Альберти.
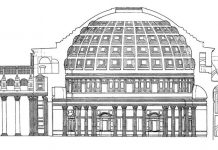
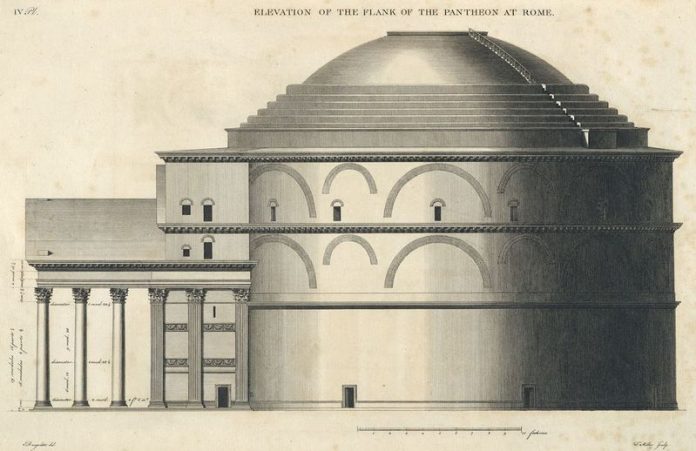
У Альберти, пытавшегося установить пропорциональные связи, то есть аналогии, между различными видами прямолинейных фигур естественно должно было родиться стремление распространить эти закономерности, являвшиеся для него выражением «органической» связи между частями целого, на качественно различные явления, то есть установить соотношение между такими противоположностями, как круг и квадрат, криволинейное и прямолинейное. Качественная аналогия, обогащавшая познание и расширявшая его горизонты, переходила в количественную пропорцию, закреплявшую эту аналогичную связь. Когда теоретики искусства Возрождения говорили о «пропорциях» как основном средстве познания действительности, то их декларации не следует понимать как утверждение отвлеченно-количественного изучения явлений действительности.
«Пропорция», не следует забывать, была для них «аналогией». Достаточно напомнить такое заявление Луки Пачоли в его «Summa arith- meticae»: «Философы прекрасно знали, что никакая вещь в природе не может быть понята без пропорций, ибо все наше изучение стремится к тому, чтобы установить отношение одной вещи к другой»; «Пропорцией в обычном смысле является деятельность сопоставления двух вещей друг с другом с одной точки зрения».43 Альбертиев- ские определения по аналогии были именно такого рода логическими «пропорциями», а его теоретико-познавательный метод находился в полном соответствии с теми требованиями, которые Альберти предъявлял к совершенному произведению искусства и которые заключались в органической целостности частей, объединенных единством «пропорций», то есть аналогией или подобием их.