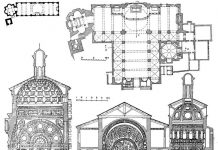
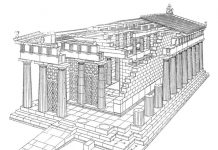
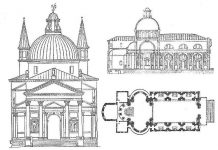
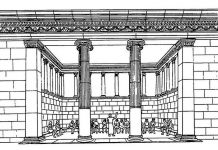
Для Альберти была дорога идея связи, середины, одинаково удаленной от крайностей, — «золотой середины», которую воспел Гораций,10 11 а не «золотое сечение» в техническом смысле слова.
Была ли позиция Альберти в вопросе о «золотом сечении» лишь его индивидуальной? Ответу на этот вопрос следует предпослать краткий исторический обзор источников, трактовавших о «золотом сечении». Он покажет, что в этом отношении Альберти был не одинок, что до исследований Цейзинга никто систематически не разрабатывал проблемы «золота» применительно к архитектуре, даже Лука Пачоли, автор трактата «О божественной пропорции», не показал, каким же образом богословско-математическая теория «золотого сечения», изложенная им в первой части, связывается с тем витру- вианским, по существу модульным, архитектурным каноном, который составляет предмет последней книги трактата.12
Основными античными источниками по интересующим нас вопросам являлись и для Средних веков, и для эпохи Возрождения «Начала» Евклида и «Тимей» Платона.13
В «Началах» теоремы, связанные с «золотым сечением», имеются во второй, шестой и трех последних книгах.14 Происхождение этих теорем на основании исследований последних десятилетий рисуется так. Исследования Евы Закс,15 Э. Франка16 и других полностью рассеяли легенду об обширных математических познаниях древнейших пифагорейцев. Проблема иррациональных величин и «золотого сечения» стала актуальной проблемой в пифагорейских кругах лишь в IV в. до н. э. Платон в своих «Законах», вряд ли написанных ранее 360 г., свидетельствует устами Афинянина, что в более широких образованных кругах в это время еще ничего не было известно о проблеме иррационального и что он сам лишь поздно и недавно познакомился с нею.17 Из диалога «Теэтет» явствует, что первым знакомством с этой проблемой афиняне обязаны геометру Феодору и что оно относится ко времени незадолго до 399 г. до н. э.. В том же диалоге «Теэтет» проводится различение величин, соизмеримых «по длине», цт]К£1 стццетрси, и соизмеримых «в степени», 5\)v&pei а\>цц£Тро1, то есть рациональных и иррациональных.18 Диалог посвящен памяти математика Теэтета, погибшего в 369 г. Этому Теэтету и должен быть приписан ряд связанных с «золотым сечением» теорем, содержащихся в «Началах» Евклида,19 а именно теорема о сторонах шести- и десятиугольника и построение пяти правильных тел, которое в переводе на современный алгебраический язык сводится к следующему соотношению между сторонами многогранников и радиусом описанного шара
Дальнейшая разработка проблем связана с именем Евдокса. В комментарии Прокла к «Началам» Евклида сохранена цитата из Гемина, согласно которой Евдокс «умножил число теорем о [золотом] сечении, ведущих начало от Платона, и пользовался аналитическим методом при их доказательстве». Утверждение о Платоне как основоположнике теории золотого сечения исторически недостоверно, сочинение Евдокса до нас не дошло, но «Начала» Евклида сохранили евдоксовы теоремы XIII, 1-5,21 которые в алгебраическом выражении, при
18 Рациональные числа соизмеримы, то есть имеют общую меру, будучи взяты в первой степени. Иррациональные квадратные корни становятся соизмеримыми, будучи возведены в квадрат, то есть во вторую степень. Хэмбидж берет термин «Динамическая симметрия» в этом смысле: «Несоизмеримость линий, но соизмеримость площадей — вот что является отличительной чертой динамической симметрии». Однако он вкладывает в это понятие еще иной смысл, противопоставляя динамику статике и называя соизмеримость или «симметрию» первой степени — статической симметрией.
Закс замечает: «По-видимому, даже ко времени после Теэтета учение о золотом сечении не полностью еще было разработано, ибо теорема: „сторона правильного десятиугольника есть больший отрезок разделенного в золоте радиуса описанного круга» еще не находит применения у Евклида. Возможно поэтому, что и открытие построения „золотого сечения» относится к более позднему времени, чем полагали до сих пор».23
Из числа других теорем, помещенных в «Началах» Евклида, следует привести еще XIII, 6, устанавливающую следующую наглядную связь между сторонами правильных многогранников : «Если квадрат, построенный на диаметре шара, описанного около этих пяти тел, разделить на шесть равных частей, то квадрат, построенный на стороне тетраэдра, равен четырем таким частям, октаэдра — трем, куба — двум. Из остальных же двух, коих отношение к другим и отношение между собою нерациональны, сторона икосаэдра больше стороны додекаэдра».
Дальнейшее развитие теории правильных многогранников может быть прослежено по книгам XIV и XV «Начал» Евклида, на самом деле не принадлежащим ему. В книге XIV, принадлежащей Гипсик- лу, имеется теорема, опять-таки связанная с теорией многогранников : «Если какая-нибудь прямая разделена в крайнем и среднем отношении, то сумма квадратов, построенных на целой прямой и большем отрезке, относится к сумме квадратов, построенных на целой и на меньшем отрезке, как ребро куба относится к ребру икосаэдра». Что же касается так называемой книги XV Евклида, то, по всей вероятности, она написана учеником Исидора Милетского, одного из строителей Константинопольской Софии.25 В теореме 7 прямо назван «наш великий учитель Исидор, которому приписывается открытие способа определять наклонения плоскостей в пяти правильных телах»,26
Теоремы Евклида о «золотом сечении», за исключением только что указанных двух, без доказательств, см. в книге: Архитектура античного мира / Сост. В. П. Зубов и Ф. А. Петровский. М., 1940. С. 296-299.