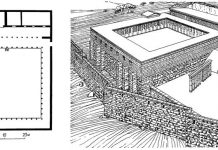
Галилей берет случай горизонтальной балки из однородного материала, имеющей прямоугольное сечение, закрепленной одним концом и нагруженной на другом конце вертикальной силой Р. Он представляет себе силу приложенной к плечу как бы коленчатого рычага АОБ, имеющего точку опоры на нижней грани балки в точке О. Действие этой внешней силы уравновешивается действием внутренних элементарных сил, которые Галилей мыслит себе равными, равномерно распределенными по всей площади F поперечного сечения балки и противящимися растяжению тела: равнодействующая сила S проходит через центр сечения В, который можно представить себе как конец другого плеча коленчатого рычага АОВ.
Основываясь на этих предпосылках, Галилей рассматривает явления сначала «отвлеченно и отдельно от материи»,8 а потом, учитывая вес рычага, то есть связи с материей. Он исследует случаи, когда изменяется одна лишь длина и одна лишь толщина балки, случай одновременного изменения длины и толщины, а также ряд случаев, производных от основных, видоизменяя установленные им основные формулы.
Таковы основные положения и факты, с которыми оперировал Галилей. Вопрос о том, каким путем он пришел к своим выводам. Оказывается, что и для него важнейшую роль сыграло альбертиев- ское представление о балке как поперек положенной колонне. В самом деле, с чего Галилей начинает? В «первом дне» «Бесед» участники рассуждают о том, как «найти для всех металлов, камня, дерева, стекла и т. д. ту предельную длину цилиндров, которые можно сделать из них в виде нитей или стержней любой толщины, сверх которой они уже не будут держаться и разрываются от собственного веса».9 Галилей приводит любопытный опыт с медной проволокой, к которой привешен груз. Если предположить, например, что наибольшим грузом, который она выдерживает, являются 50 футов, то эти 50 футов, «прибавленные к собственному весу проволоки, равняющемуся, скажем, восьмушке унции, и вытянутые в проволоку той же толщины, дадут проволоку предельной длины, которая только в состоянии держаться».10 11 Таким образом, Галилей начинает с вертикально поставленной тяжести, которую он сближает с вертикально подвешенным грузом. Показательно, что, рассматривая вопрос о причине связности частей твердого тела, Галилей начинает с веревки, затем переходит к дереву, а затем уже к камню и металлу. «Подобно тому, как в веревке мы приписываем ее сопротивляемость множеству составляющих ее нитей пеньки, так и в дереве мы находим продольные волокна и нити, делающие его более прочным, нежели пеньковая веревка той же толщины. Что касается цилиндров из камня или металла, то еще большая связность их частей зависит от другой причины, отличной от нитей и волокон, но и эти материалы также могут быть разорваны сильным растягиванием»,и
Лишь во «втором дне» «Бесед» собеседники переходят к горизонтальным балкам. Здесь ставится вопрос, почему «твердые цилиндры или призмы из стекла, дерева или иного ломкого материала, будучи подвешены вертикально, выдерживают весьма большой груз, в то время как при горизонтальном положении […] они могут быть сломаны малым грузом».12 Характерно, что и здесь продолжают появляться сравнения с веревкой, на которой подвешен груз. Так, Симп- личио, участник диалога, стоящий на старых аристотелевских позициях и играющий в диалоге роль недоверчивого вопрошателя, высказывает предположение, что «длинный канат менее способен выдерживать большой груз, нежели короткий», а потому сопротивление должно уменьшаться в телах по мере их удлинения и притом «не только при поперечном изгибе, но и при продольном растяжении».13 Сальвиати, выразитель мыслей самого Галилея, правда, опровергает мнение своего собеседника, но тем не менее из контекста совершенно очевидно, что и в случае горизонтальной балки внутренние элементарные силы мыслятся неизмелившимися, одинаково распределенными по всей площади поперечного сечения балки, как и в случае вертикально подвешенной веревки. Так, при выводе формулы для балок одинаковой длины, но разной толщины, Галилей- Сальвиати исходит из мысли, что сопротивление одного цилиндра во столько раз превосходит сопротивление другого, во сколько раз его основание больше основания другого, «потому что во столько же раз многочисленнее и волокна, нити или другие элементы, связывающие часть твердого тела».14 Словом, Галилей мыслит внутренние силы в горизонтальной балке тождественными силе сопротивления растяжению в вертикально расположенном теле. Именно это было одним из обстоятельств, лишивших Галилея возможности прийти к идее нейтрального слоя и к правильному определению абсолютной величины напряжения. Как замечает А. Н. Долгов,15 в действительности наибольшее напряжение втрое больше для прямоугольных балок, чем полагал Галилей, и в четыре раза больше для массивных цилиндрических балок, однако это различие обусловливается лишь разницей в коэффициентах. «Если поэтому отвлечься от абсолютной величины напряжения и отыскивать только, „в каком отношении оно находится у подобных между собой и несходных друг с другом призм и цилиндров из одного и того же материала, но имеющих различную длину и толщину», как это делает.
Дальнейшая история вопроса есть не что иное, как постепенная модификация и уточнение этой исходной аналогии.
В1684 г. Лейбниц в сочинении «Demonstrationes novae de resistetia solidorum»16
попытался внести коррективы в галилеевские рассуждения. Однако он продолжал исходить из тех же аналогий, что и Галилей, лишь усложняя и дифференцируя их. Ошибка последнего, по Лейбницу, в том, что он представлял себе балку «абсолютно жесткой », переламывающейся в один момент сразу, как только преодолено ее сопротивление, между тем перелому и разрыву предшествует изгиб и растяжение, которые различны в различных волокнах, образующих балку. Подобно Галилею, Лейбниц представляет себе балку состоящей как бы из волокон, но силы сопротивления, в отличие от Галилея, мыслит различными в различных волокнах, а именно возрастающими по мере приближения к верхней грани балки, пропорционально квадрату их расстояния от нижней.
Рассуждение Лейбница ведется примерно так. Когда брус расположен вертикально и к концу его подвешен груз, растяжение и сопротивление каждого из волокон одинаковы; поэтому при АС=СК сопротивление пропорционально площади квадрата АВКС. Когда брус расположен горизонтально и одним своим концом вделан в стену, внутренние силы каждого волокна, по предположению Галилея, остаются теми же, а момент сопротивления по закону рычага пропорционален расстоянию каждого волокна от точки опоры А; иначе говоря, момент сопротивления волокна ВК будет относиться к моменту сопротивления волокна HL, как АВ к Aff. Так как АВ :АН = ВК: НМ и так как рассуждение применимо ко всем волокнам, то момент сопротивления всех волокон выразится площадью треугольника АВК, равной половине площади квадрата АВСК. Лейбниц вносит в рассуждения Галилея ту поправку, что наряду со сказанным сами внутренние силы меняются пропорционально расстоянию волокон от точки опоры. Тогда моменты сопротивления в отдельных волокнах будут пропорциональны уже не расстояниям, а квадратам расстояний АВ, АН и т. д., момент же сопротивления всех их будет пропорционален площади NRSQN, где NQS есть дуга параболы. Если обозначить максимальное расстояние АВ через if, а меняющиеся расстояния других волокон принять за переменное Л, то по галилеевской версии момент сопротивления всех волокон будет равен определенному интегралу
Еще дальше, чем Лейбниц, пошел Мариотт в сочинении, впервые опубликованном в 1690 г.17
Мариотт основывался и на теоретических рассуждениях, и на экспериментах, им произведенных. Подобно Галилею и Лейбницу, Мариотт представлял себе тела состоящими из волокон.18 Подобно Лейбницу, он признавал, что силы сопротивления в различных волокнах различны при горизонтальном положении балки и возрастают по мере приближения к верхней грани ее.19 И наконец, в отличие от Лейбница, он подошел к представлению о «нейтральном слое»; при изгибе в верхних волокнах происходит растяжение, а в нижних — сжатие, для которого требуется усилие.20
Уже из беглого обзора с очевидностью явствует, что наука о сопротивлении материалов пришла к правильным представлениям в результате слияния двух теоретических течений, развивавшихся независимо друг от друга. Первый путь начинал с аналогий между силами, действующими в горизонтально и вертикально расположенном теле. Оставляя вне поля зрения ряд существенных различий, эти аналогии позволили прийти к первым количественно-математичес- ским определениям соотношения между силой, объемом, формой, массой. Представления об изменчивости внутренних сил, упругость балки оставались в стороне. Эти представления развивались независимо и лишь постепенно просочились в круг понятий, в пределах которого разрабатывались первые начатки теории сопротивления материалов. Любопытным примером чисто качественного анализа явлений упругости являются рассуждения Даниеле Барба- ро в его «Комментариях к Витрувию»21. Облеченные в схоластическую форму, они с трудом поддаются адекватной передаче на русском языке. Барбаро исходит из понятия lenitudo, охватывающего и гибкость твердых тел, и тягучесть или вязкость жидких. Понятию lenitudo противопоставляется жесткость rigiditas, определяемая как способность «противодействия изгибу и искривлению». Все эти определения носят у Барбаро чисто качественный характер. Пытаясь объяснить только что установленную разницу между телами, он прибегает к гипотезе о присутствии в телах особого рода влаги, обладающей силой «цепкости» и «клейкости». Эта влага может быть «тонкой » и « воздушной », тогда в ней преобладают свойства растяжимости и, наоборот, более «грубой», тогда в ней преобладают свойства стягивания и сцепления. Трудное изложение Барборо легче всего понять, если на место двух «влаг» поставить две силы — растягивающую и стягивающую: обе влаги лишь результат мышления сил в образе жидкостей. Тела, согнутые от природы» и принимающие согнутую форму после своего выпрямления, имеют с внутренней стороны сгиба «стягивающую уплотненную влажность», возвращающую их к первоначальному виду. Иное — в телах, которые выпрямляются сами собой после искривления.
«Те тела, которые прямы и по искривлении сами собою выпрямляются, способны, благодаря тому что влага в них тонкая и клейкая, несколько растягиваться в длину, но там, где в этих членах есть клейкость грубая, там присутствует своего рода сила сцепления и стягивания; поскольку эта влага имеет силу сцепления и гибкости и допускает растяжение, она делает возможным изгиб на наружной стороне без излома, а поскольку она густая и обладает силой стягивания, тело при отпускании принимает прежнюю форму. Если грубая часть влаги допускает искривление на выгнутой стороне, а на вогнутой происходит при этом сжатие, то более тонкая часть влаги, которая скорее является воздухом, чем водою, в этой части сжимается; при устранении силы тела сами собою выпрямляются, ибо стягивающее начало на выгнутой наружной стороне стягивается, а тонкая часть влаги на вогнутой внутренней стороне растягивается и теснит сцепляющие части, заставляя тело выпрямляться».
Словом, если высвободить понятие силы из его образной оболочки, то анализ Барбаро сведется к анализу сил, действующих на выгнутой и вогнутой поверхности. Как ни элементарны и наивны в своей основе эти рассуждения, они с самого начала ставят вопрос о разнице действия внутренних сил в верхней и нижней части балки или другого какого-либо сгибаемого тела. Отсюда открывается путь к мысли о «нейтральном слое».
Если бы Галилей силой своей абстракции не оторвался от конкретной сложности явления и не начал бы с альбертиевской схемы «балка — поперечно положенная колонна» — он остался бы на той до-количественной стадии, на которой остановился Барборо. Отвлеченная аналогия, игнорирующая явления упругости и изменчивость внутренних сил, привела его к первым количественным законам теории сопротивления материалов. То путь, на котором Галилей пришел к своим выводам, сам по себе не мог, однако, привести его к дальнейшему постижению явления во всей его сложности. Качественно новые представления должны были прийти извне. В этом была эвристическая ценность аналогии и в этом же ее ограниченность. Одна отвлеченная аналогия, оторвавшись от конкретного содержания, могла превратиться в тормоз познания. В связи с конкретным созерцанием, в цепи развивающихся аналогий, обогащающаяся, развивающаяся, усложняющаяся, она превращалась в могучую силу.