Альберти при своей конкретизации к поискам количественных соотношений между частями органического целого: нужно было найти такое соответствие, которое позволяло бы по одной части «размерить все прочие». Музыкальные аналогии точно так же вели в конечном итоге к числу. Коренное различие между ними и аналогиями органическими заключалось в том, что музыкальная теория строго ограничивала Альберти кругом целых и рациональных чисел.
Неправ, однако, Мишель, утверждая, что Альберти отдавал исключительное предпочтение «музыкальным числам, то есть целым и простым отношениям», что «числа иррациональные, „золотое сече- ние“, „божественная пропорция» Пачоли, по-видимому, неизвестны нашему автору».6 Альберти пользовался иррациональными отношениями. Так, высота дверей определяется у него как диагональ квадрата, сторона которого равна ширине двери. Длина пандуса оказывается иррациональным числом при указываемом Альберти отношении вертикали к горизонтали, равном 1 : 6. Наконец, геометрическое среднее, о котором говорит Альберти, по большей части также выражается иррациональными числами. Но вместе с тем ясно видно, что он старался по возможности избежать иррациональностей; так, например, указывая пропорции атриумов и следуя здесь Витрувию, он заменил указываемое античным автором отношение >/50 :5 рациональным отношением >/49 : 5 или 7:5.7
Вместе с тем Альберти проявляет полное равнодушие к тому, что сторона правильного вписанного десятиугольника равна большей части радиуса, разделенного в крайнем и среднем отношении, хотя и считает десятиугольный участок «весьма пригодным и красивым» и указывает правило построения вписанного десятиугольника.
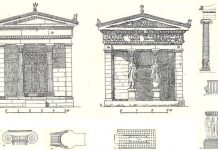
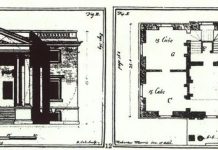
Указанную особенность мышления Альберти можно видеть и на следующем примере. Витрувий определяет для коринфской капители величину абака тем, что «диагонали, проведенные от одного угла к другому, будут вдвое длиннее высоты капители», которая равна в свою очередь нижнему диаметру колонны; иначе говоря, сторона абаки по Витрувию равна d4i • Альберти дает следующий расчет: «Высота капители коринфян равна нижнему диаметру колонны. Вся эта высота делится на семь модулей… Ширина абаки занимает десять модулей».8 9 Нетрудно видеть, что указания Альберти и Витрувия по существу совпадают, так как 10А есть приближенное значение .9
Сначала о филологической стороне вопроса. Указание высоты зданий для участка с соотношением сторон 4:1 подозрительно прежде всего потому, что в отличие от всех других случаев сначала указывается высота зданий при сводчатых перекрытиях, а лишь затем — при плоских. Напрашивается предположение, не ошибка ли это и не следует ли переставить слова «сводчатые» и «плоские» соответственно порядку, принятому во всех остальных случаях. Это предположение подкрепляется тем, что иначе для h в случае а = 3ft и а = 4ft получается одно значение: 7А b. Если произвести перестановку, изменится высота и в следующих двух случаях, так как об одном из них говорится, что высота здания будет как и при отношении 4:1, а о другом — «как в предыдущем случае». Во-вторых, отмечавшееся нами как двусмысленное положении, что мы имеем дело с приближенным указанием иррациональных значений квадратных и кубических корней в рациональных числах.
Веским аргументом в пользу расшифровки величин ll/i2 а как \]ab2
представляется, на наш взгляд, то, что именно этой же самой приближенной величиной Альберти пользовался при построении своей «идеальной» башни.
Таким образом, таблица 1 может быть представлена в следующем алгебраически-обобщенном виде. Подкреплением ее правильности служат слова Альберти : «Этим средним [то есть арифметическим, геометрическим и музыкальным] архитекторы чаще всего пользовались для определения высоты сооружения».
Получается логически стройная картина, стройность которой увеличивается еще более, если вспомнить, что Альберти рассматривает случаи не в том порядке, в каком они даны в таблице, а по группам, которые приближаются к группам, объединяемым однородными формулами. Сначала он рассматривает случаи 7-11, когда высота строится по геометрической пропорции ‘Jab. Далее он говорит об остальных случаях, начиная с первого, причем на самый конец оставляет участки с более сложным соотношением сторон, а именно 7 : 5 и 5 : 3. В обоих последних случаях, очевидно, во избежание еще более сложных отношений при выведении высоты Альберти пользуется самым простым средним, то есть арифметическим. Тем же средним он пользуется в случае 3, когда Ъ имеет также дробный коэффициент Уз.
Высоту h при равенстве длины и ширины можно рассматривать и как арифметическое среднее и как простое равенство всех трех измерений. Интересно, что в этом случае Альберти дает и другой вариант: полудиагональ квадрата. С этим случаем сближается случай 5, когда h есть сторона равностороннего треугольника с высотою, равной Ь. Особняком стоит случай 2. Порядок изложения в части сводчатых перекрытий подчиняется основному порядку изложения для плоских перекрытий, а потому в нем как таковом меньше стройности.
Из всего сказанного следует два вывода, как бы ни относиться к предложенной конъектуре, относящейся лишь к одному случаю из одиннадцати. Во-первых, Альберти гораздо шире пользовался иррациональными величинами, чем это принято было думать, — гораздо шире даже, чем это было отмечено в нашем комментарии. Во-вторых у Альберти чаще всего выражал иррациональные «геометрические» величины в округленных рациональных числах, что сильно затруднило их выявление.
Историки математической науки отмечали, что античные математики никогда не ставили себе целью знакомить своих читателей с методами своей эвристической работы. Откуда математик брал то или иное решение — это его личное дело, «секрет производства».14 Это замечание вполне применимо к теоретикам архитектуры Ренессанса, в том числе к Альберти. Как бы ни относиться к заявлениям Альберти, что он писал для ремесленников,15 писал ли он действительно для ремесленников или же для заказчиков, ясно, что Альберти редко знакомил читателя с теми операциями, путем которых он пришел к своим выводам. Вместо того чтобы предоставить читателю самому произвести те или иные математические вычисления или произвести расчеты у него на глазах, Альберти предпочитал дать готовую цифру, готовое число, сразу применимые на практике. Поэтому его указания, касающиеся архитектурных пропорций, носят на первый взгляд случайно-эмпирический характер, и для того чтобы проникнуть вглубь, до его системы пропорционирования, требуется такая же аналитическая работа по расшифровке, как и при изучении пропорций непосредственно по самим архитектурным памятникам.
За последние 5-10 лет в среде наших архитекторов и искусствоведов заметно оживился интерес к вопросам архитектурных пропорций. Наряду с переводами иностранных сочинений были опубликованы и работы советских исследователей, а еще большее количество самых различных «систем пропорционального анализа» так и не увидело света. На первых порах изучение пропорций среди молодых и неопытных «пропорциеведов» нередко сводилось к эмпирическому констатированию наличия тех или иных математических соотношений в архитектурном памятнике или к выжиманию при помощи циркуля особо излюбленных пропорций, например «золота». Такое абстрактное занятие, не требующее особой затраты исследовательской энергии, вызвало естественную реакцию и даже породило несколько недоверчивое отношение к проблеме архитектурных пропорций вообще. Лишь постепенно созрела мысль о необходимости улавливать не отдельные пропорции или соотношения, не factum brutum,4)
а систему пропорционирования в целом, мысль о необходимости понять своеобразную логику архитектурного пропорционирования. На конкретном материале, преимущественно классических памятниках, были сделаны подчас весьма остроумные попытки расшифровать различные пропорциональные системы зодчества. Однако и подобные системы большинства как наших, так и зарубежных исследователей оставляют чувство неудовлетворенности по той причине, что самый метод раскрытия подобных систем по существу своему является не аналитическим, а синтетическим. Это уясняется из следующего примера. Каждое число может быть представлено в виде суммы разных слагаемых, например, можно представить число 6 и как сумму 1 и 5, и как сумму 2 и 4, и как сумму 3 и 3 и т. д. Приблизительно то же имеет место в подобных системах: они показывают, как могли возникнуть те или иные пропорции целого, но не гарантируют того, что они действительно возникли именно так, ибо такие системы синтетически идут от произвольно выбранных элементов к целому; в таком случае почти всегда можно путем выбора самых элементов или слагаемых разными путями прийти к желанному результату: 1 + 5 действительно равно 6,нои2 + 4иЗ + 3 также равно 6. Главный же вопрос заключается в нахождении именно первичных элементов, слагаемых, а они могут быть обнаружены только аналитически. Если и здесь прибегнуть к сравнению, то придется привести в качестве примера разложение числа на первоначальные множители. Такое разложение приводит всегда к однозначному результату, вслед за которым возможен и обратный путь, синтетический, служащий проверкой — от найденных элементов к целому.
Подобными первичными элементами в интересующем нас вопросе являются те элементарные технические приемы пропорциониро- вания, которые должны быть обнаружены уже не путем всегда гадательного формально-теоретического исследования, «прощупывания циркулем», а лишь путем исторического анализа. Одной из существенных опор исторического анализа являются дошедшие до нас письменные источники, далеко не изученные до сих пор во всей полноте. Словом, нужно доходить до «первоначальных множителей», а не подбирать и комбинировать произвольно выбранные слагаемые.