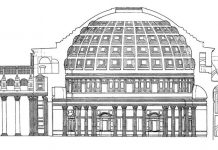
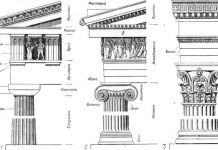
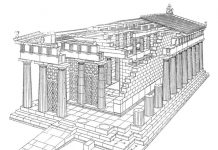
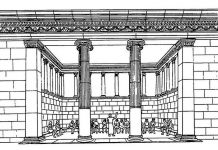
Витрувий, говоря о дорических колоннах, вовсе не упоминает о базе, так как предполагает известным, что дорические колонны бывают без базы. Альберти придает дорическим колоннам аттическую базу. По Витрувию, длина и ширина аттической базы — 11/2 £>, Альберти дает два варианта, или, точнее, верхний и нижний предел для их величины: IV2D и lVzD. Указание о величине листеля и скоции у Витрувия отсутствует. Для дорической капители Альберти дает два варианта: один — близкий к Витрувию, другой — на основании наблюдений над древними зданиями. В отличие от Витрувия Альберти делит дорический архитрав на пояса. Тэния архитрава у Витрувия, соответствующая верхнему поясу Альберти, равна W модуля, а не Vi, как у Альберти. У Витрувия нет речи о «шнуре овалов» над фризом.
В ионическом ордере расхождения таковы. Высота плинта ионической базы, по Витрувию, такая, как в аттической : высота его у Альберти — Vi высоты базы, то есть Vs D. Витрувий, следуя греческим образцам, не делает нижнего вала в базе, а верхний вал делает толще, чем Альберти. Наряду с витрувианским вариантом базы Альберти дает другой вариант, на основании собственного обмера древних зданий. Построение ионической капители у Витрувия и Альберти обнаруживает ряд сравнительно мелких расхождений. Киматий ионического архитрава по Витрувию — Vi его высоты, по Альберти — %. Наряду с витрувианским архитравом Альберти описывает и другой на основании собственных наблюдений. Для фриза Витрувий указывает две величины: ЪА и ЬА архитрава. Альберти — одну: высоту, равную высоте архитрава. Киматий фриза по Витрувию — У? его, по Альберти — 1А или Уь. Значительно расходятся величины киматия дентикула: Ув высоты последнего, по Витрувию, 3А — по Альберти. Некоторые расхождения обнаруживаются и в высоте симы.
Наконец, в коринфском ордере пропорции капителей у Витрувия и Альберти совпадают, за исключением отдельных мелочей. При характеристике антаблемента Альберти упоминает о модельонах, отличительных для позднеримской эпохи.26
Таким образом, во всех трех ордерах система числовых отношений берется готовой, в своей эмпирической данности, либо из текста Витрувия, либо из древних памятников. Попыток объяснить происхождение или логику этой системы не делается. Только в одном случае имеется у Альберти намек на подобную попытку. Указав, по Витрувию, пропорции аттической базы, а именно: высота базы— V2Z), ширина плинта — % Z), высота плинта — Уз высоты базы, Альберти делает вывод: «Высота всей базы была, следовательно, тройной по отношению к высоте плинта, а ширина плинта также тройной по отношению к высоте базы». Иными словами, Альберти хочет сказать, что высота базы Н есть средняя пропорциональная между шириной плинта и его высотой.
Немаловажно, что в отличие от Витрувия, для которого ширина плинта равна только % D, у Альберти указаны две величины: «Плинт должен был быть в длину и в ширину таков, каков нижний диаметр колонны, с придачей не больше половины и не меньше трети этого диаметра», то есть от 4/з D до % D. Напрашивается предположение, не рассматривает ли Альберти эти две величины как приближенное значение .
Следовательно, в этом едва ли не единственном случае Альберти попытался возвести числовые указания Витрувия к их предполагаемому геометрическому источнику: к диагональному построению и к излюбленному у него самого понятию среднего пропорционального.
При построении ионической волюты Альберти пользовался полуокружностями, а Витрувий — четвертями окружности.
Как бы то ни было, совершенно очевидно, где именно следует и где не следует искать элементы собственной оригинальной архитектурной геометрии Альберти.29
Спрашивается, почему при всем геометризме основных приемов пропорционирования Альберти в такой мере тяготел к музыкальноархитектурным, числовым аналогиям.
На первый взгляд кажется, что «арифметизация» архитектурных пропорций, замена иррациональных отношений геометрии приближенными значениями, выражаемыми в рациональных числах, уводила Альберти от живой практики архитектурного искусства и ее чувственно-наглядной «геометрии». Действительно, он порою впадал здесь в области музыкальных аналогий, в известный схематизм. Тем не менее такой перевод линий в число имел для Альберти первостепенное значение.
Стоит ли указывать, что пользование целыми числами вместо иррациональных преследовало цели чисто практические: упростить изложение и сделать указания доступными каждому практику. Этот мотив был весьма веским для всех теоретиков Ренессанса при выборе «модульной системы изложения». Такие же тенденции наблюдаются и в других писаниях того же времени, например в гномонике. Даниеле Барбаро, давая указания, как строить солнечные часы, «прячет» теорию, то есть математические доказательства, от любознательного практика, и только во втором итальянском издании несколько приподнимает завесу, воспроизведя комментарий Коммандино к трактату Птолемея об аналемме.30 Нечто аналогичное должно было иметь место и в архитектуре. В своих «Математических забавах» Альберти равным образом не доказывал и даже не указывал теорем, на которых основаны его практические советы.
Но этого мало. Арифметизация «очертаний», перевод их в числа были средством добиться наглядной сравнимости элементов, обеспечить измерение и соизмерение их. Перевод lineamenta в числа был одним из способов проверки и обнаружения ошибок, хотя Альберти прекрасно сознавал, что его могло «обмануть и число». Полагаю излишним подробнее останавливаться и в этой роли архитектурной арифметизации и «омузыкаливания».
Существеннее третий момент: переосмысление пропорциональных соотношений путем перевода их в числа. Понять, что значит «пере- осмысливание», поможет взгляд, брошенный в прошлое музыкальной теории. Обобщая и несколько схематизируя, можно было бы наметить две основные струи в античной музыкальной науке: рационалистическую и эмпирическую, или, назовем их условно, «пифагорейскую» и «аристоксеновскую». Пифагорейская школа оперировала отвлеченно-трактованными числовыми соотношениями; начиная с простых целых чисел, она в конечном итоге уходила в дебри сложных и мелких числовых отношений, нередко даже ускользавших от чувственного восприятия. В противоположность им Аристоксен исходил из звукового восприятия, считая возможным нивелировать мельчайшие акустические различия и приходя в конечном итоге к своеобразной системе темперации. Обе тенденции хорошо охарактеризованы Боэцием, сочинение которого, как уже указывалось, было известно Альберти: Пифагор был философ, «не веривший никаким человеческим ушам ».31 Аристоксен, наоборот, «все суждение предоставлял целиком ушам ».32 Сам Боэций занял посредствующую позицию, пытаясь обосновать ее ссылкой на авторитет «пифагорейцев», которых он отличает от самого Пифагора: « Они не целиком предоставляют суждение ушам, но тем не менее кое-что исследуют не иначе, как посредством ушей. А именно самые созвучия они определяют ухом, тогда как о расстояниях между созвучиями предоставляют судить не ушам, суждения которых тупы, а правилам и разуму, чтобы чувство было как бы подчиненным и слугой, судьей же и повелителем был разум. Ибо хотя элементы всех почти искусств, да и самой жизни, обязаны своим происхождением чувствам, однако в чувствах не будет никакого надежного суждения, никакого постижения истины, если отступится от них приговор разума».33 По Альберти, точно так же красота чувствуется непосредственно или, как он говорит, сразу. «Все мы, ученые и неученые, от природы чувствуем сразу, что в искусствах и вещах есть хорошего и дурного». «Чувство зрения острее других», и все «недоделанное, шаткое, лишнее, пустое или несуразное» тотчас же «приводит нас в волнение», заставляя желать, чтобы оно стало прекраснее. «Когда гармоничное, путем ли зрения или слуха, или как-нибудь иначе, предстанет перед душою, мы его чувствуем сразу». Вместе с тем Альберти пытался установить геометрические и числовые законы гармонии и прекрасного, «сразу» воспринимаемые зрением. Когда, следовательно, Альберти обращался за проверкой чувственно-воспринимаемой гармонии к числу, он поступал подобно музыкантам школы Боэция.