Мог найти у Августина. Августин устанавливал градацию геометрических фигур и линий с точки зрения их большей или меньшей близости к единству: прямая линия совершеннее ломаной или кривой потому, что в ней больше единства; равносторонний треугольник совершеннее равнобедренного по той же причине; квадрат совершеннее равностороннего треугольника, так как в нем равные стороны лежат против равных сторон, а в равностороннем треугольнике равные стороны лежат против равных углов, то есть в нем меньше равенства или «справедливости» ; наконец, еще больше равенства в круге, где нет разницы между диагоналями и сторонами, как в квадрате, и где все линии, проведенные из середины к краям, одинаковы. Понятие единства лежало у Августина и в основе симметрии, как соответствия равного равному. Словом, по сжатому определению самого Августина, — Omnispulchritudinis forma unitas est [Форма всякой красоты — единство].* 7
Отзвуки этой теории можно усмотреть у Альберти. Однако то конкретное содержание, которое он вкладывает в свои формулы, существенно отлично. Характерно, что умозрительное обоснование Августина он заменил апелляцией к живому организму. У Августина эстетика в конечном счете устремлялась к сверхчувственному Единому неоплатоников.8
Для Альберти последним критерием является наглядный образ живого существа, то есть единого во многом.
Если художественное произведение, по Альберти, есть «как бы живое существо», то оно не может быть только единым, а должно быть единым во многом. Иными словами, части, отличаясь друг от друга, должны все же образовать некое единство. Если все части равны друг другу, то это единство выражается в пространственном соответствии их друг другу, в симметрии. Принцип симметрии у Альберти обосновывается в отличие от Августина не ссылкой на понятие единства или равенства, а на образец организма. «Кости здания, то есть колонны, углы и тому подобное, наши предки, следуя природе, делали в четном числе. Ведь ты не найдешь животного, которое стояло бы или передвигалось на ногах, нечетных по числу. Наоборот, отверстия они нигде не делали в четном числе, что, как можно видеть, соблюдается и природой, ибо хотя у живых существ уши, глаза и ноздри расположены в четном числе по правую и левую сторону, но посредине — отверстие одно и широкое». «Если собаке приделать на голове ослиные уши или если у кого-нибудь одна огромная нога или одна рука большая, а другая крохотная, то все они будут безобразны. Один глаз голубой, а другой — черный считаются некрасивыми даже у животных: настолько естественно, чтобы правое соответствовало левому полной своей однородностью». Из этого Альберти делает вывод, что правое должно в точности соответствовать левому, «верхнее — нижнему, родственное — родственному, равное — равному для украшения того тела, частями которого они будут». «Даже статуи и картины и все украшения необходимо прилаживать так, чтобы они находились на свойственных им, наиболее подходящих местах и казались как бы близнецами».
Требование о соответствии «равного равному» Альберти повторяет неоднократно.9
Знаменательно, что этот принцип соответствия равного равному имел для Альберти, как и принцип единства, не только эстетическое, но и техническое значение. Например, клинья арки «должны быть соответственно равными, чтобы, словно на весах, правое соответствовало левому видом, величиной, тяжестью и тому подобным». «Все станет бесполезно, если при сложении не будут тщательно соблюдаться порядок и мера. Ибо все в отдельности должно быть сведено к числу так, чтобы равное соответствовало равному, правое — левому, верхнее — нижнему».
В требовании подобного равенства Альберти заходил весьма далеко, указывая, например: «Наблюдали также за тем, чтобы не было ни одной колонны, ни базы, ни капители, ни стены, которые не были бы совершенно сходны со всеми прочими того же ордера по высоте и ширине, по всем размерам и виду ». Такое указание явно противоречит живым вариациям в величине интерколумния, хотя бы, например, колоннад Парфенона и иных величайших произведений мирового зодчества, всем тем refinements, о которых писал Гудьир и другие авторы. Если к этому добавить, что, по мнению Альберти, ставить колонны отвесно «совершенно необходимо как с точки зрения прочности, так и с точки зрения красоты»,10 11 то нельзя не усмотреть в подобных требованиях Альберти проявление своеобразного теоретического ригоризма, которому он вряд ли оставался верен и в своем художественном восприятии, и в своей художественной практике, в особенности если вспомнить приведенные выше цитаты, свидетельствующие о его «плененности» разнообразием вещей.
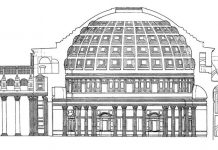
В тех случаях, когда части неравны, наступает принцип подобия или пропорциональности: большие части должны быть пропорциональны меньшим. Примером может служить построение триумфальной арки. Вся ширина арки равна 8 модулям, ширина среднего пролета равна 2 модулям, <расстояние> до пяты арки равно 2 Уз модуля, из чего приходится заключить, что вся высота равна 2 Уз + 1 модуль = 3 Уз модуля. Иными словами, средний пролет вписывается в прямоугольник с отношением сторон 3 Уз: 2 или 5 : 3. Далее Альберти говорит: «То же соотношение будет и у частей, примыкающих к боковым пролетам одинакового размера».
В своей архитектурной практике Альберти соблюдал тот самый принцип соответствия частей, о котором он так выразительно сказал по поводу триумфальной арки. Что в основе фасада Сан Франческо в Римини лежит мотив триумфальной арки, общеизвестно. Интересно, что именно здесь соблюден и принцип подобия. Хорошо об этом говорит Франкль: «Гордость Альберти составляло соблюдение одной пропорции для арок. Средняя арка шире, но поэтому и выше, чем боковые арки; абсолютные размеры различны, но пропорции все-таки остаются друг другу равными».11 Так возникающие фигуры называются в элементарной геометрии «подобными фигурами». Посредством подобных фигур создается впечатление теснейшей связности и глубочайшей родственности, более того, необходимости и незыблемости целого; члены, имеющие различную величину и тем не менее подобные друг другу, становятся членами целостного организма, одушевленного единым духом. Альберти имел это в виду, когда говорил о «музыке отношений».12
Наконец, если части не равны и не подобны друг другу, то возникает необходимость связать их друг с другом посредством промежуточного звена. Так мы приходим к понятию среднего пропорционального, или «среднего».
В «Тимее» Платона отчетливо определено это понятие связующего среднего: «Невозможно, чтобы две вещи совершенным образом соединялись без третьей, так как между ними должна появиться связь, которая скрепляла бы их. Это наилучшим образом может выполнить пропорция, ибо если три числа, тяжести или силы, обладают тем свойством, что среднее так относится к последнему, как первое к среднему, и, наоборот, последнее так относится к среднему, как среднее к первому, то последнее и первое будет средним, а среднее — первым и последним. Таким образом, все по необходимости будет тем же самым, а так как оно будет тем же самым, то оно составит целое».
Впрочем, незачем даже обращаться к Платону. Связи Альберти с ним, как было указано, более далеки, чем с другими мыслителями древности, например Аристотелем. Прежде чем приводить некоторые мысли Аристотеля, напомним, каким образом Альберти предваряет свое изложение трех видов «среднего» — арифметического, геометрического и музыкального. «Существуют правила, — говорит он, — весьма полезные, изобретенные как музыкантами, так и геометрами и людьми, занимающимися арифметикой, которые неплохо усвоить. Философы здесь предлагали название „среднее», но виды „среднего» и разнообразны и многочисленны. У ученых есть три основных способа получить среднее; цель всех их — когда есть два крайних числа, найти третье число, соответствующее двум другим определенным образом, то есть, если можно так выразиться, связанное с тем и другим узами родства ».13
Таким образом «среднее» — своего рода «узы родства», объединяющие разнообразные части художественного целого.
Аристотель различал два вида « среднего» или «средины » : «средину» в самом предмете и «средину» по отношению к нам. Под срединой самого предмета следует разуметь то, что равно отстоит от обоих концов; таково, например, среднее арифметической пропорции ): число шесть, например, настолько же больше двух, насколько меньше десяти. Средина самого предмета «всегда одна и притом одна и та же во всех предметах». Средина «по отношению к нам » есть «то, что не дает ни излишка, ни недостатка», и эта средина «не одна и та же для всех». «Если для кого-либо 10 фунтов пищи слишком много, а 2 фунта — слишком мало, то учитель гимнастики не прикажет ему есть 6 фунтов, потому что и это количество может оказаться для такого лица или слишком большим, или слишком малым: [силачу] Милону этого слишком мало, а начинающему заниматься гимнастикой — слишком много. То же самое и относительно бега и состязаний. Каждый знающий человек избегает излишества и недостатка и стремится к середине и избирает ее, и притом не среднее по отношению к самому предмету, а по отношению к нему. Если всякая наука тем путем достигает хороших результатов, что имеет в виду середину и к этой середине направляет свои действия, и если хорошие мастера работают, как мы сказали, имея в виду середину, и если добродетель выше и лучше всякого искусства, то и она точно так же, как и природа, должна стремиться к середине».3)
Эту большую цитату я был вынужден привести не только потому, что в ней содержится прямое указание: «хорошие мастера работают, имея в виду середину». Она содержит также существенное сближение между «срединой» и понятием совершенства, отличительным признаком которого является невозможность что-либо отнять или что-либо прибавить. Аристотелевское определение совершенства — основное у Альберти.
В несколько ином аспекте, но, по существу, в том же смысле, понятие «среднее» берется у Альберти в пятой книге: «Ведь ясно, что природу во всех вещах радует умеренность; да и самое здоровье — не что иное, как соразмерность всех составных частей, а среднее всегда доставляет удовольствие». В комментарии я указывал на параллельное место у Галена, определявшего здоровье как соразмерное сочетание влажного, сухого, теплого и холодного начал. Но можно было бы указать и другое место у того же Галена,14 где говорится, что лучшие произведения художника бывают тогда, когда они стремятся к середине.
Уже после напечатания Комментария мне удалось в сочинениях Боэция обнаружить ближайшие параллели к трактату Альберти.16 Источником Боэция является Никомах, различение этих трех видов среднего повторялось и другими античными и средневековыми авторами, но естественнее всего предположить, что Альберти почерпнул это различение именно у Боэция, сочинения которого в Средние века лежали в основе школьного образования, тем более, что другие сочинения античных авторов, у которых Альберти мог бы почерпнуть то же различение, вряд ли были доступны ему.17
Интересно, что пифагорействующие математики древности довели число «средних » до «совершенного» числа пифагорейцев — 10, а Альберти из всех 10 «средних» уделил внимание только трем. Ниже приводятся эти 10 пропорций по Боэцию.18
Во втором столбце приведены harmonica, Альберти остался верен своему стремлению обойтись без грецизмов. Самое слово «гармония» он заменил в своем трактате латинским concinnitas.