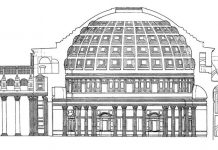
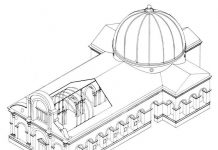
Альберти не только стремился установить зрительно приемлемую связь между противоположностями или объединить в одно родовое логическое понятие различные виды центрических сооружений, его отличало стремление путем выбора надлежащих величин установить количественно выразимые связи между противоположным: он совершенно явно оперировал спрямленными дугами окружности. Так, высота стены до начала свода в круглых храмах делалась «наиболее опытными зодчими» равной n/u диаметра, то есть спрямленной четверти окружности, при значении к = 22Л.31
Другой пример — окна сенаторской курии: «Высоту оконных отверстий делят на одиннадцать равных частей, из них семь частей будут предоставлены ширине». Очевидно, что высота окна есть в данном случае спрямленная полуокружность с диаметром, равным ширине окна при значении к = 22Л.32 ’AvaXoyia была в данном случае не только качественным сходством, но и количественным соответствием, пропорциональностью, имевшей целью закрепить органическое единство частей.
Весьма вероятно также пользование спрямленными частями окружности при построении чимбии и нижнего апотесиса колонны. Величина радиуса AF, который на V? меньше нижнего радиуса, получается очень просто путем построения как высота равностороннего треугольника со стороной, равной нижнему радиусу. Эта высота h = -^у-Я. Взяв приближенное значение л/3 = 12Л, получаем для нее %. Величина АН определяется у Альберти в тексте в три модуля. ЛинияАС, проводимая от руки, «имеет своим началом четверть маленького круга ». Радиус этого круга, по указанию Альберти, равен высоте листели, то есть модулю. Уже Тейер указывал, что требование Альберти о начале линии в виде четверти маленького круга «конструктивно невыполнимо», а я в своем комментарии высказывал предположение, что Альберти лишь приблизительно хотел наметить характер изогнутой линии. Не отказываясь и теперь от этого предположения, считаю возможным толковать слова « eius istius flexionis initium quartam habebit circuli pusilli — начало этого изгиба будет иметь четверть маленького круга» и в другом смысле: спрямленная четверть окружности определяет точку на кривой. При радиусе т и значении к = 22А спрямленная четверть окружности будет равна иЛ т. Из точки В засекаем с этим раствором циркуля точку Е. Тогда BD будет дуга окружности радиуса1 Vi т, равного четверти окружности СВ. Интересующая нас кривая будет в своем начале примерно совпадать с дугой окружности BD, давая более правдоподобный и плавный ход, нежели движение по дуге маленького круга ВС. При таком толковании лучше объясняется и наличие слова quartam, так как очевидно, что вся четверть маленькой окружности никак не может являться началом кривой. Такое построение, наконец, ближе подходит к тем построениям, которыми пользовался в своем комментарии к Витрувию Даниеле Барборо. Определяющей для Барборо является дуга круга с центром проходящая через обе точки d и Ь; как и у Альберти, круг лишь приблизительно намечает ход вычерчивания от руки линии, которую Барборо называет «изящнейшей».33
Интерес к знаменитой задаче о «квадратуре круга», к ее хотя бы приближенно грубому решению в известной степени и в известных кругах не мог не обусловливаться подобным стремлением практически объединить противоположности, установить соответствие между ними, то есть установить пропорциональность и аналогию.34
Свидетельством о непосредственных занятиях Альберти этими вопросами служит отрывок «О квадратуре луночек», опубликованный Манчи- ни.35 Отрывок, написанный по-итальянски, начинается со следующего заявления: «Вопреки мнению многих, кто говорит, что для фигур, ограниченных кривыми линиями и дугами не существует точной квадратуры, в особенности же для тех фигур, которые являются частями круга, и кто утверждает это, по моему мнению, на основании авторитета Аристотеля, который говорит, что quadratura circuli est scibilis sed non scita quia impotentia naturae,36 и кто из невозможности точной квадратуры круга делает вывод о невозможности точной квадратуры фигур, очерченных кривыми линиями или дугами, как сказано выше, я тем не менее нашел точную квадратуру фигуры, здесь начерченной» — и далее следует рассуждение.