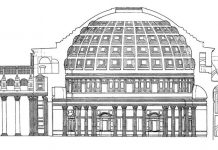
Творчество Палладио дает наиболее убедительный пример подобного понимания архитектурной симметрии.
В эпоху Ренессанса возрождаются традиции древней геометрии, в то же время исчезает числовой эзотеризм средневековья, «божественные» числовые закономерности уступают место «антропоморфным».
Однако столетия спустя традицию построения тончайших «звездчатых схем» средневековья уже при анализе закономерностей геометрии в архитектуре прошлого продолжает в XX в. норвежский археолог Лунд. Изучив и сравнив планы большинства европейских готических соборов, Лунд обнаруживает в них «двойной квадрат» и «золотое сечение» -следствие геометрических построений, сочетающих в центрической композиции пятиугольник, квадрат и равносторонний треугольник.
Севильский кафедральный Собор Приседения Святой Марии
Наблюдая постоянство традиционных представлений о гармонии, симметрии, зафиксированных в текстах теоретиков архитектуры эпохи Ренессанса, подмечаем особенность: XV век — время подведения итогов, осмысления истории новой архитектуры как длящейся традиции. «Рационализм литературного восстановления античного опыта, логической реконструкции утверждает себя в архитектуре как единственная форма рационализма.
Речь идет о рассуждающем архитекторе, своего рода юристе, способном обосновать любое свое решение отсылкой к авторитету. «Судить правильно о том, что подобает» (Альберти) — это древняя формула в новом смысле слов «правильно» и «подобает» привнесена в архитектуру эпохой Возрождения и без изменений унаследована традицией Просвещения, обратившейся вновь к языку классики».
В эпоху Возрождения, когда классицизм переживал начальный период своего рождения, достижения античности использовались в той мере, в какой они соответствовали идеалам гуманистов.
Альберти вслед за Витрувием понимает красоту как целостное соотношение частей или гармонию, образованную числом. Числа же -продукт разума, божественного или человеческого.
Он разделяет представления о том, что природа служит лишь материалом, из которого боги творят красоту, полную разума и души: природе как идеальной конструкции и подражают произведения искусства, служат ее символами. Однако Альберти был чужд антропоморфизм, который мы обнаруживаем, например, у Франческо ди Джорджо Мартини.
На рисунках этого зодчего-теоретика в колонну вписана фигура девушки, в капитель человеческая голова. Иначе поступает Альберти; для него, как и для эпохи в целом, характерно не столько изображение человеческого тела, сколько постижение его закономерностей, которые приводятся к числовым.
Зодчие-гуманисты, восприняв развитую неоплатониками идею антропоморфного микрокосма, в соответствующем смысле истолковали отрывок из трактата Витрувия о хорошо сложенной фигуре человека, которая своими пропорциями может уподобляться совершенным геометрическим формам.
Числовыми пропорциями, извлеченными из совершенной человеческой фигуры, по мнению зодчих Ренессанса, следовало руководствоваться при строительстве и здания, и города в целом. Это побуждало к составлению аналитических чертежей фигуры человека, вписанной в круг и квадрат, разработке модульных величин для проектирования.
Принцип подобия и взаимосвязи части и целого, лежащий в основе неоплатонических представлений о макро- и микрокосме, в область архитектуры и градостроительства перенес Альберти, развивший мысль, высказанную Платоном: «Приятно было бы видеть город, имеющий облик единого дома».
Альберти писал, что «государство, по мнению философов, величайший дом и, обратно, дом есть самое мелкое государство». И далее: «Дом есть маленький город». Крепость, по его мнению, в функциональном отношении должна быть уменьшенной копией города, а главная башня в центре цитадели, в свою очередь, «будет как бы меньшей крепостью».
Принцип подобия и взаимосвязи части и целого
В диссертации, посвященной архитектурной теории Альберти, В. Зубов акцентирует те представления зодчего, которые мы относим к «идеям симметрии»: «…идея единства и множества, целого и частей выступает у Альберти на первый план.
Соответствие частей друг другу берется не только в широком качественном смысле, как у средневековых схоластических философов (например, у Фомы Аквината с его пониманием красоты как «должного соответствия», debita proportio, или «расположения», отвечающего природе, dispositio naturae conveniens).
Альберти, в соответствии с традициями мастеров-практиков, уделяет большое, если не наибольшее внимание количественной стороне проблемы, вопросу о числовом и метрическом соответствии частей друг другу, т. е. вопросу о пропорциональности в точном значении этого слова».
Альберти определяет «concinitas» -латинский перевод греческого слова «симметрия» как закономерное соответствие, согласование всех частей здания, которое нельзя нарушить без ущерба для его красоты. Здание можно считать симметричным, если отношение его элементов друг к другу выражено при помощи «правильной», «истинной» формулы. Архитектура становится как бы наглядной, изображенной формулой гармонии. Эту мысль позднее неоднократно будут повторять теоретики строгого классицизма во Франции (XVII в.).
Ренессанс сохраняет и отчасти воскрешает структурно-математическое понимание красоты, для него характерен тщательный анализ всех арифметических и геометрических соотношений любого произведения искусства, своего рода математический структурализм, восходящий к античному пифагорейскому платонизму. Однако, по тонкому замечанию А. Лосева, «в сравнении с возрожденческой детализацией вопроса вся античность представляется наивным детством. Вот почему пифагорействующий платонизм Ренессанса с точки зрения всемирно-исторического процесса является переходом от античной наивно-зрительной космологической эстетики к математическому естествознанию XVII в.».